Overview

Membership attributes in LDAP entries create a directed graph of entries that can contain cycles. Having cycles in membership makes almost no sense and add complexity. This is the reason why memberof plugin assums that the directed graph is actually an acyclic directed graph and enforce during evaluation of the graph that there is no cycle.

The nodes of the graph are directed by membership attributes (member, uniquemember, memberuser…) that are represented by blue arrows in the figure below. MemberOf plugin manages the values of LDAP attribute memberOf into the graph. This attribute creates an other graph with direct edges from a node to all the nodes it is member of, represented by red arrows.

acyclic directed graph

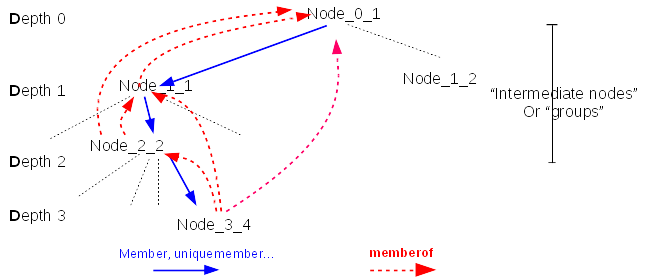
When updating a group, MemberOf plugin needs to update the memberof attribute of several nodes. To do so, it does two actions:

Those two actions are necessary but can be expensive in terms of:

This document presents some possible improvements.

Use Case

An administrator needs to provision many entries (leafs or groups) within a fixed period of time(typically over a week end). He can use CLI or batch commands or even importing entries from a ldif file. The rate of the provisioning is critical to be sure to complete the task in an acceptable delay.

Design

Simplifications

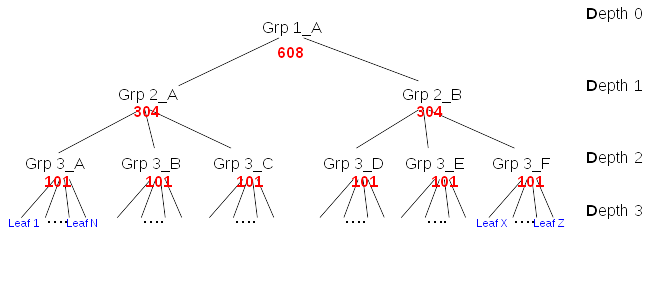
The graph of membership can be very complex. For simplification, this document will evaluate the impact of membership update on limited types of graphs with same leaf depth:

Membership graph

Membership graph

Membership graph

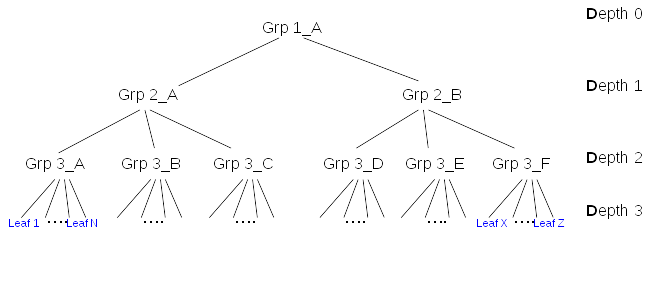
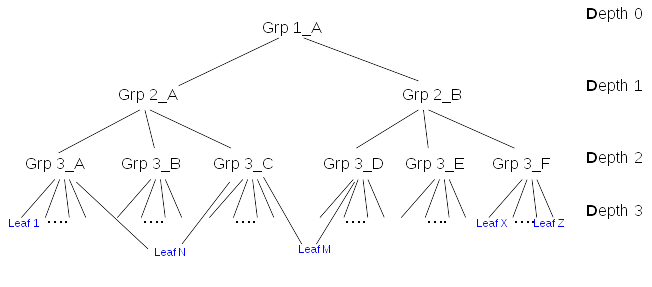
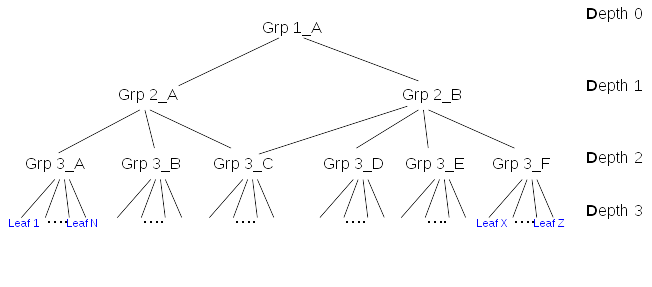
Cost of memberof update

Tests done with Nested groups provisioning shown that by far the main contributor was the Number of internal searches. For example with a total of 10000 leafs creating 400 nested groups tiggered 14M internal searches.

The initial thought that the update of the entry (fixup) was the main responsible of preformance hit, was not completely right. Update of the member entry (to update memberof) has IO cost but IO is not that main contributor. For example, in the same test case, disabling retroCL, that divides IO by factor 2 had no significant impact on provisioning duration.

So in the rest of the document the cost will be expressed in terms of internal searches.

Membership graph

The figure above shows a membership graph. At the bottom of the graph leafs are typically users. Those users are directly member of a group of Depth 3 (i.e. Grp3_A), for example Grp 3_A is ‘Devel Kernel Group’. Then this group is member of Depth 2 group (i.e. Grp 2_A) like ‘Framework Devel Group’. This group is member of Depth 1 group (i.e. Grp 1_A) like ‘Engineering’.

Algorythm

When a group is updated, to add/del/moddn members, Memberof plugin updates the attribute memberof of all entries that are impacted by the update of the group. The graphs is look down from the target group down to the leafs to retrieve the impacted nodes. During the look down, each impacted node is fixup. The fixup of node consist of

look down

The look down uses the following search for all impacted nodes (leaf or intermediate node) 

SRCH base="<node_dn>" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs="attr_1 ... attr_N"
attr_1,...,attr_N: are membership attributes (defined in "cn=MemberOf Plugin,cn=plugins,cn=config")

This internal base search is very rapid at the condition node_dn remains in the entry cache. If the entry is a group (i.e. attr_x exists), it recurses for all the members. When the entry is a leaf it fixup the entry ( look up + update of memberof ). When the entry is a group and all its members have been fixup, then the group itself is fixup ( look up + update of memberof ).

Note that during look down, a same entry can be found several times. This happens when it exists multiples paths from the original updated group to a node belonging to its membership graph.

During a updating (MOD) the members of a group, the look down contains searches: 

# retrieve the targeted group
SRCH base="<group_dn>" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL
SRCH base="<group_dn>" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL

# then for each impacted node
SRCH base="<impacted_node_dn>" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL

look up

When a group is updated, for each impacted members it computes all the groups containing (direct or indirect) the impacted members. So for each given impacted member (leafs and intermediate nodes) it does an internal search for each node from the impacted member up to the root. 

SRCH base="<suffix>" scope=2 filter="(|(attr_1=<node_dn>)..(attr_N=<node_dn>))" attrs=ALL
attr_1,...,attr_N: are membership attributes (defined in "cn=MemberOf Plugin,cn=plugins,cn=config")
They are supposed to be indexed in equality

For example with a path: Grp_1_A -> Grp_2_A -> Grp_3_C -> Leaf_N. The access log will contain
SRCH base="<suffix>" scope=2 filter="(|(attr_1=<Leaf_N>)..(attr_N=<Leaf_N>))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=<Grp_3_C>)..(attr_N=<Grp_3_C>))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=<Grp_2_A>)..(attr_N=<Grp_2_A>))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=<Grp_1_A>)..(attr_N=<Grp_1_A>))" attrs=ALL

Assuming that attr_1,..,attr_N are indexed in equality, the searches are fast but items that can influence the cost are

update

The update of the impacted node is done with an internal MOD. It can be caught by other plugins that can search the entry. For example mep plugin triggers for each update: 

SRCH base="<impacted_node_dn>" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL

Methodology

A typical update (update a Level Grp_3 group, to add 5 leafs) produces the those set of operations

    #
    # Modify cn=group_0 to add 5 leafs user_601...user_605
    #
conn=2 op=5 MOD dn="cn=group_0,ou=groups,dc=example,dc=com"
    conn=Internal  SRCH base="cn=group_0,ou=groups,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  SRCH base="cn=group_0,ou=groups,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0

    # Look down for user_601
    conn=Internal  SRCH base="uid=user_601,ou=people,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs="member uniquemember"
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0

    # fixup: Look up for user_601
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=uid=user_601,ou=People,dc=example,dc=com)
                (uniquemember=uid=user_601,ou=People,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_0,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_0,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_10,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_10,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_30,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_30,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=0 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0

    # Fixup: update for user_601
    conn=Internal  MOD dn="uid=user_601,ou=People,dc=example,dc=com"
    conn=Internal  SRCH base="uid=user_601,ou=People,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=0 etime=0

    # Look down for user_602
    conn=Internal  SRCH base="uid=user_602,ou=people,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs="member uniquemember"
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0

    # fixup: Look up for user_602
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=uid=user_602,ou=People,dc=example,dc=com)
                (uniquemember=uid=user_602,ou=People,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_0,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_0,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_10,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_10,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_30,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_30,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=0 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0

    # Fixup: update for user_602
    conn=Internal  MOD dn="uid=user_602,ou=People,dc=example,dc=com"
    conn=Internal  SRCH base="uid=user_602,ou=People,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL

    ...


    # fixup: Look up for user_605
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=uid=user_605,ou=People,dc=example,dc=com)
                (uniquemember=uid=user_605,ou=People,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_0,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_0,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_10,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_10,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_30,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_30,ou=Groups,dc=example,dc=com))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=0 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0

    # Fixup: update for user_602
    conn=Internal  MOD dn="uid=user_605,ou=People,dc=example,dc=com"
    conn=Internal  SRCH base="uid=user_605,ou=People,dc=example,dc=com" scope=0 filter="(|(objectclass=*)(objectclass=ldapsubentry))" attrs=ALL
    conn=Internal  RESULT err=0 tag=48 nentries=1 etime=0
    conn=Internal  RESULT err=0 tag=48 nentries=0 etime=0

    # end of the MOD add of the 5 leafs user_601..user_605
conn=2 op=5 RESULT err=0 tag=103 nentries=0 etime=0

In this example, we can see look down searches, as well as look up searches and update search. Also we can see that some look up searches are identical searches. For example, the following search appears 5 times in the example (one time for each added leaf).

    conn=Internal  SRCH base="dc=example,dc=com" scope=2 
        filter="(|(member=cn=group_30,ou=Groups,dc=example,dc=com)
                (uniquemember=cn=group_30,ou=Groups,dc=example,dc=com))" attrs=ALL

In each of the following paragraphs, we will present various kind of updates (MOD add/del/replace leafs/groups, ADD groups and DEL groups). For each kind of update the evaluation will follow the template:

MODIFY Adding ONE leaf as member of a group

The use case is a modify(group_DN, [(ldap.MOD_ADD, ‘member’, leaf_DN)]).

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains NO identical search.

Without identical searches, there is no optimization to do for that use case:

In conclusion:

MODIFY Deleting ONE leaf from being member of a group

The use case is a modify(group_DN, [(ldap.MOD_DELETE, ‘member’, leaf_DN)]).

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains NO identical search.

Without identical searches, there is no optimization to do for that use case:

In conclusion:

MODIFY Replacing ONE leaf with an other leaf as member of a group

The operation on the updated group is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains NO identical search.

Without identical searches, there is no optimization to do for that use case:

In conclusion:

MODIFY Adding N leafs as members of a group

The use case is a modify(group_DN, [(ldap.MOD_ADD, ‘member’, [leaf_1_dn,…,leaf_N_dn)]).

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches.

For example adding the N leafs to Grp_3_A, the update of the group triggers

# N times the search
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_A)..(attr_N=Grp_3_A))" attrs=ALL

# N times the search
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N times the search
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

For example N leafs being member of Grp_3_C, add them to Grp_3_D

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# N times the search for path Grp_3_D->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# N times the search for path Grp_3_D->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# For path Grp_3_D->Grp_2_B->Grp_1_A, there is no search for Grp_1_A because it is common
# node with previous path Grp_3_C->Grp_2_A->Grp_1_A

For example N leafs being added to Grp_3_C

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# For path Grp_3_C->Grp_2_B->Grp_1_A, there is no search for Grp_1_A because it is common
# node with previous path Grp_3_C->Grp_2_A->Grp_1_A

If we can prevent identical searches, doing a single search of the intermediates nodes, the cost would be reduced by:

In conclusion:

MODIFY Delete N leafs as members of a group

The use case is a modify(group_DN, [(ldap.MOD_DELETE, ‘member’, [leaf_1_dn,…,leaf_N_dn)]).

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches.

For example, assuming N leafs members of Grp_3_A and Grp_3_C, if those N leafs are suppressed from Grp_3_A

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

If we can prevent * identical searches , doing a single search of the *intermediates nodes, the cost would be reduced:

In conclusion:

MODIFY Replace N leafs with N others as members of a group

The operation on the updated group is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches:

For example, assuming N leafs are new members of Grp_3_A

# N times the search for path Grp_3_A->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_A)..(attr_N=Grp_3_A))" attrs=ALL

# N times the search for path Grp_3_A->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N times the search for path Grp_3_A->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

For example, assuming N leafs remain member of Grp_3_C and N leafs are new members of Grp_3_C and Grp_3_D

# For N removed leafs that are now only member of Grp_3_C
   # N times the search for the path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

   # N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

   # N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# For N added leafs that are now member of Grp_3_C and Grp_3_D
   # N times the search for the path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

   # N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

   # N times the search for path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

   # N times the search for the path Grp_3_D->Grp_2_B->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

   # N times the search for path Grp_3_D->Grp_2_B->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# For path Grp_3_D->Grp_2_B->Grp_1_A, there is no search for Grp_1_A because it is common
# node with previous path Grp_3_C->Grp_2_A->Grp_1_A

For example assuming N leafs are new member of Grp_3_C

   # N times the search for the path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# Grp_3_C being member of Grp_2_A, it evaluates this path
   # N times the search for the path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

   # N times the search for the path Grp_3_C->Grp_2_A->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# Grp_3_C is also member of Grp_2_B, it evaluates this path
   # N times the search for the path Grp_3_C->Grp_2_B->Grp_1_A
   SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# For path Grp_3_C->Grp_2_B->Grp_1_A, there is no search for Grp_1_A because it is common
# node with previous path Grp_3_C->Grp_2_A->Grp_1_A

If we can prevent identical searches , doing a single search of the intermediates nodes, the cost would be reduced by:

In conclusion:

MODIFY Adding N groups to a group

The use case is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches:

For example, adding Grp_3_B and Grp_3_C as members of Grp_2_A then N=2.

# M+1 times the search for path Grp_3_B->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_B)..(attr_N=Grp_3_B))" attrs=ALL

# N(M+1) times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# M+1 times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N(M+1) times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

For example, Grp_3_D and Grp_3_E have the exact same set of leafs than Grp_3_C, Grp_2_B has one member that is Grp_3_F. use case is add Grp_3_D and Grp_3_E as members of Grp_2_B (so N=2)

# N*M times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N*M times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N*M + 1 times the search for path Grp_3_D->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# N*M + 1 times the search for path Grp_3_E->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_E)..(attr_N=Grp_3_E))" attrs=ALL

# N(M + 1) times the search for path Grp_3_E->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# N(M + 1) times the search for path Grp_3_E->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

For example, Grp_3_C and Grp_3_D are members of Grp_2_A but not member of Grp_2_B. The use case is to add Grp_3_C and Grp_3_D to Grp_2_B.

# N*M + 1 times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N*(M + 1)times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N*(M + 1) times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# N*M + 1 times the search for path Grp_3_D->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# N*(M + 1) times the search for path Grp_3_D->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

If we can prevent identical searches , doing a single search of the intermediates nodes, the cost would be reduced by:

MODIFY Deleting N groups to a group

The use case is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches:

For example, removing Grp_3_B and Grp_3_C from Grp_2_A

# M+1 times the search for path Grp_3_B
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_B)..(attr_N=Grp_3_B))" attrs=ALL

# M+1 times the search for path Grp_3_C
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

For example, Grp_3_D and Grp_3_E have the exact same set of leafs than Grp_3_C, Grp_3_D and Grp_3_E are members of Grp_2_B. The use case is remove Grp_3_D and Grp_3_E as members of Grp_2_B (so N=2)

# N*M times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# N*M times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N*M times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# N*M + 1 times the search for path Grp_3_D
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# N*M + 1 times the search for path Grp_3_E
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_E)..(attr_N=Grp_3_E))" attrs=ALL

For example, Grp_3_C and Grp_3_D are members of Grp_2_A and also members of Grp_2_B. The use case is to remove Grp_3_C and Grp_3_D from Grp_2_B.

# M + 1 times the search for path Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# M + 1 times the search for path Grp_3_D->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# N(M + 1) times the search for path Grp_3_C/Grp_3_D->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N(M + 1) times the search for path Grp_3_C/Grp_3_D->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

If we can prevent identical searches , doing a single search of the intermediates nodes, the cost would be reduced by:

MODIFY Replace N groups with N others as members of a group

The use case is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches:

For example, in Grp_2_A replacing Grp_3_B and Grp_3_C with Grp_3_G and Grp_3_H

# M+1 times the search for path Grp_3_B
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_B)..(attr_N=Grp_3_B))" attrs=ALL

# M+1 times the search for path Grp_3_C
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# M+1 times the search for path Grp_3_G
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_G)..(attr_N=Grp_3_G))" attrs=ALL

# M+1 times the search for path Grp_3_H
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_H)..(attr_N=Grp_3_H))" attrs=ALL

# N*(M+1) times the search for path Grp_3_G->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N*(M+1) times the search for path Grp_3_H->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

For example, replace in Grp_2_B, Grp_3_D and Grp_3_E with Grp_3_B and Grp_3_C (so N=2)

# M+1 times the search for path Grp_3_B
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_B)..(attr_N=Grp_3_B))" attrs=ALL

# M+1 times the search for path Grp_3_C
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# M+1 times the search for path Grp_3_D
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# M+1 times the search for path Grp_3_H
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_E)..(attr_N=Grp_3_E))" attrs=ALL

# N*(M+1) times the search for path Grp_3_B/Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# N*(M+1) times the search for path Grp_3_B/Grp_3_C->Grp_2_A->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# N*(M+1) times the search for path Grp_3_B/Grp_3_C->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

If we can prevent identical searches , doing a single search of the intermediates nodes, the cost would be reduced by:

ADD group entry

The use case is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches:

For example, ADD a Grp_0_A group that has only one member Grp_1_A

# 6*(M+1) times the search for path Grp_3*-->Grp_0_A, for the intermediates node <x> in A,B,C,D,E,F
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_<x>)..(attr_N=Grp_3_<x>))" attrs=ALL

# 2*3*(M+1) + 1 times the search for path Grp_2_*-->Grp_0_A, for the intermediates node <x> in A,B
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_<x>)..(attr_N=Grp_2_<x>))" attrs=ALL

# 1*6*(M+1) + 3 times the search for path Grp_1_A-->Grp_0_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# 1*6*(M+1) + 3 times the search for path Grp_0_A->Grp_0_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_0_A)..(attr_N=Grp_0_A))" attrs=ALL

For example, ADD a Grp_0_A group that has only one member Grp_1_A

# 2 * (2M + 1) time the search for Grp_3_C->root and Grp_3_D->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL

# 4 * (M + 1) time the search for Grp_3_<x>->root with <x> in [ABEF]
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_<x>)..(attr_N=Grp_3_<x>))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_<x>)..(attr_N=Grp_3_<x>))" attrs=ALL

# 2 * (4M + 4) time the search for Grp_2_A->root and Grp_2_B->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# 2 * (6M + 9) time the search for Grp_1_A->root and Grp_0_B->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_0_B)..(attr_N=Grp_0_B))" attrs=ALL

For example, ADD a Grp_0_A group that has only one member Grp_1_A

# 2*(M+1) times the search for path Grp_3_C->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_C)..(attr_N=Grp_3_C))" attrs=ALL

# 5*(M+1) times the search for path Grp_3_* (except Grp_3_C) ->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_*)..(attr_N=Grp_3_*))" attrs=ALL

# 4*(M+1) + 1 times the search for path Grp_2_A ->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_A)..(attr_N=Grp_2_A))" attrs=ALL

# 5*(M+1) + 1 times the search for path Grp_2_B ->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL

# 7*(M+1) + 3 times the search for path Grp_1_A ->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

# 7*(M+1) + 3 times the search for path Grp_0_A ->root
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_0_A)..(attr_N=Grp_0_A))" attrs=ALL

If we can prevent identical searches , doing a single search of the intermediates nodes, the cost would be reduced by:

DEL group entry

The use case is

The look down costs (with those searches) in that case are

The fixup cost is the cumul of costs of look up (searches) and update(searches).

The fixup cost contains several identical searches:

For example, DEL Grp_2_A

# 3*(M+1) times the search for path leafs-->Grp_2_A for <x> in [A, B, C]
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_<x>)..(attr_N=Grp_3_<x>))" attrs=ALL

For example, DEL Grp_2_A

# 3*(M+1) times the search for path leafs-->Grp_2_A for <x> in [A, B, C]
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_<x>)..(attr_N=Grp_3_<x>))" attrs=ALL

# 3*M times the search for path leafs-->Grp_3_D->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_D)..(attr_N=Grp_3_D))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

For example, DEL Grp_2_A

# 3*(M+1) times the search for path leafs-->Grp_2_A for <x> in [A, B, C]
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_3_<x>)..(attr_N=Grp_3_<x>))" attrs=ALL

# 2*(M+1) times the search for path leaf Grp_3_C -->Grp_3_C->Grp_2_B->Grp_1_A
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_2_B)..(attr_N=Grp_2_B))" attrs=ALL
SRCH base="<suffix>" scope=2 filter="(|(attr_1=Grp_1_A)..(attr_N=Grp_1_A))" attrs=ALL

If we can prevent identical searches , doing a single search of the intermediates nodes, the cost would be reduced by:

Conclusions

For all kind of operations on groups (ADD, DEL, MOD_ADD, MOD_DEL, MOD_REPLACE), wether the updated value(s) is/are leaf(s) or group(s),

Look down

Look down cost is the less significant part (~20%)of the overall cost, the pourcentage of the look down cost over the total cost is

      MODIFY    
  ADD DEL ADD DELETE REPLACE
Leafs - - 12-15% 15-30% 15-18%
Groups 13% 20-25% 10-15% 12-25% 13-20%
           

Look down cost is optimal regarding the following criteria:

Look down cost is not optimal when it exists several paths from the target node to some impacted nodes. For examples adding Grp_0_A with type 2, look down will find two times Leaf_N or with type 3 it will find two times all leafs of Grp_3_C. If we imagine a graph like type 3 with children of Grp_3_C being a full sub-graph all the nodes of that sub-graph will be find twice.

The ticket 48861 will prevent this duplicated effort of identifying several times the same impacted nodes. Currently, all found impacted nodes are fixup. So indentifying several times the same impacted nodes triggers several fixup of the same nodes with a useless high cost (fixup is more expensive than look down).

Fixup

fixup of a given node is split in look up of the impacted nodes and their update. The update cost is related to plugins SRCHs. In cost diagnostic, update cost was 1 SRCH per impacted entry. The look up cost is the major cost and it fluctuates depending on the graph itself. In short the more paths to the root and the longer are those paths, the more expensive it is. A approximate range is that look up is accounting for ~80% of the total cost.

The lookup is not optimal:

Reducing the in lookup cost to the the number of SRCHs strictly necessary, it would reduce lookup by:

      MODIFY    
  ADD DEL ADD DELETE REPLACE
Leafs - - 33-50% 0-33% 20-50%
Groups 60% 25-40% 50-70% 25-50% 40-60%
           

Improvements

48861: Prevent to fixup the same entry several times

When updating membership attributes of a group, the look down phase retrieves all direct and indirect impacted members of that update.

A constraint is that the graph of membership can contain several paths to a same node. For example with type 3, from Grp_1_A, all leafs of Grp_3_C will be found Twice (through Grp_1_A->Grp_2_A->Grp_3_C and Grp_1_A->Grp_2_B->Grp_3_C). The problem are:

The ticket 48861 will prevent that an impacted member is listed/fixed several times. A first patch, caching in an hash table the already fixed nodes, divides by 2 the duration of provisioning of a graph. The graph being creates with create_test_data.py. This patch is not the final one. In fact it checks duplicate effort during fixup but miss the duplicate effort during the look down.

The right patch should be done during look down because fixup will benefit of it: a impacted node being found only one time will be fixup only one time.

In addition, managing duplicate at the fixup level is useless in case of memberof fixup task where nodes are found only one time by an internal search (memberof_fix_memberof).

look down occurs during a betxn callback. The backend lock is held and in addition a memberof plugin lock (actually monitor memberof_operation_lock) is also held during look down. So only one thread (whatever the updated backend) can run look down at a given time. So we can use a single hash table to store DN of look down entries.

48856: reusing memberof current values to compute the new ones

When a group is updated, members of the group that are impacted by the update are fixup. Fixup consist of look-up and update. look-up is the most expensive part especially because, for each impacted node, it discards current memberof values and recompute them. The computation is a recursive (from impacted node to root) set of internal searchs like below:

SRCH base="<suffix>" scope=2 filter="(|(attr_1=<node_dn>)..(attr_N=<node_dn>))" attrs=ALL
attr_1,...,attr_N: are membership attributes (defined in "cn=MemberOf Plugin,cn=plugins,cn=config")

The improvement proposed with the 48856 is to avoid (as much as possible) recursive internal searches and computes the memberof values based on the memberof attribute values of their parents entries.

First proposal

This option was discussed internally and this write of is just to record the result of the discussion.

This option relies on the strong assumption that updating a node, memberof values of all parents are valid. So the way the graph is browsed will change from depth first to breadth first.

In addition the algorithm is different depending on the type of operations.

ADD, MOD_ADD or MOD_REPLACE adding values

Assuming that the parents entries have valid memberof attribute values, the impacted entries are updated based on the memberof attribute values of their parents. Look up can be completely skipped. In fact when updating a member from a parent, we just need to provide parent_DN and parent memberof. The futur memberof values of the member would be union

It basically propagates the memberof values from target to leaf.

The graphic below present the update of entry Grp_1_A to add a member Grp_2_A. Because of the requirement that parent entries have valid memberof means that the graph is processed breadth first, from the target entry. Each found node during this processing is immediately fixup. So the way the graph is look down and look up is breadth first.

Rely on parents MO value - ADD

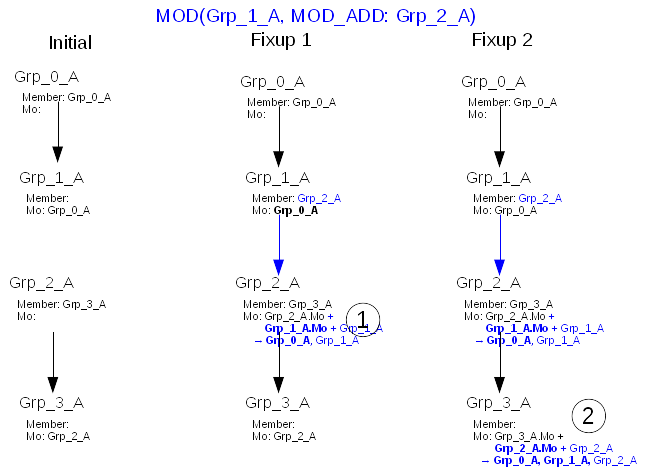
In case of ADD lookup (internal search) can be skipped as at each level the algo to update memberof value of a child is to do union (for example in graphic fixup #2 of the entry Grp_3_A)

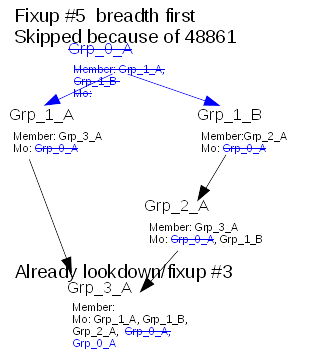
For add, detection of already fixup entry 48861 is possible.

DEL, MOD_DEL, MOD_REPLACE delete values or MODRDN

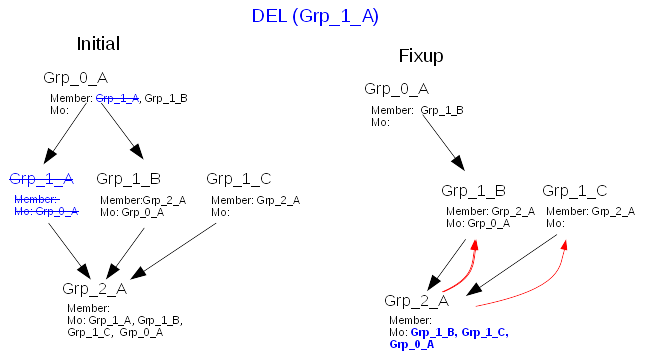
For the delete values the algo is more complex. In fact, removing values (e.g. DEL a parent) does not mean we can simply remove the values from the impacted entries. Some removed values may be granted to an impacted node through a different path. The algo is to do short lookup at the direct parent level.

In the graphic below the entry Grp_1_A is deleted. Referential integrety takes care of its membership value in Grp_0_A. Then starting look down the fixup of the impacted entry Grp_2_A is done with a “one level lookup” that computes the union of

Rely on parents MO value - DEL

Problematic case

Because of the requirement that parent entries have valid memberof values that means that the graph is processed breadth first, from the target entry. If the graph is not “balanced” it can create the following difficulty

Lets have an initial graph where we delete (in blue) the root node Grp_0_A, so memberof first fixup its child Grp_1_A

Rely on parents MO value - pb 1

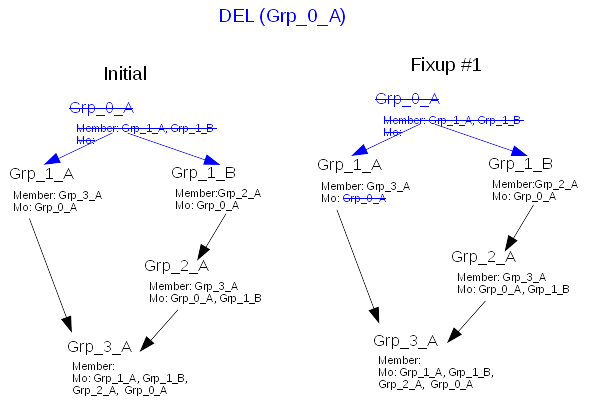
Processing the graph in breadth first, it fixup Grp_1_B (removing Grp_0_A memberof value)

Rely on parents MO value - pb 2.1

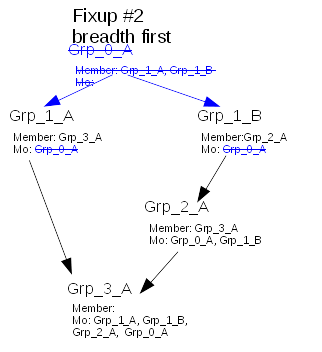
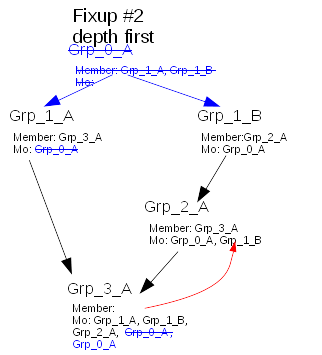
All child of Grp_0_A being fixup, it gets to the child of Grp_1_A and fixup Grp_3_A. Here running the DEL algo it computes the union of

So when processing Grp_3_A, one of its parent being not fixup, it resurrect the invalid value Grp_0_A

Rely on parents MO value - pb 2.2

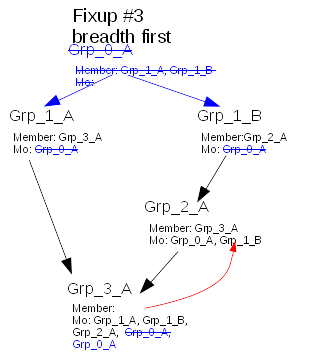
Now it completes the impacted list with Grp_2_A

Rely on parents MO value - pb 2.3

But when lookdown finds Grp_3_A, it finds that it has already been found/fixup (bug 48861) and does not fixup it.

Rely on parents MO value - pb 2.4

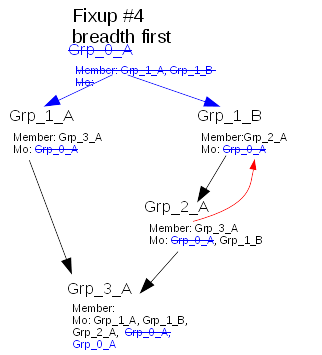
Imagine we switch to depth first after fixup of Grp_1_A, we hit the same issue

Rely on parents MO value - pb 3.1

Second proposal

This option comes from a brand new algo implemented is a python prototype.

It is still under discussion see 48856 thread. It is an approach top-down of the update that propagate the membership update impacts from root to leafs. It uses the computed memberof attribute on a given node to determine if it is necessary to propagate the update to its children. A drawback of the algo is that a given node may need to be read (updated ?) several times if there are several paths to it.

Knowing that the key factor of the performance is the number of read, we need to confirm the number of lookup/(updates).

49031: cache the parents of the groups

The vast majority of the Look up internal searches is to retrieve the parent groups of a given node.

SRCH base="<suffix>" scope=2 filter="(|(attr_1=<node_dn>)..(attr_N=<node_dn>))" attrs=ALL
attr_1,...,attr_N: are membership attributes (defined in "cn=MemberOf Plugin,cn=plugins,cn=config")

But looking at internal searches filters we can see an increasing number of them as the node_dn moves toward the root. It also fluctuates highly as soon as there are nested groups and nodes/leafs belong to several groups.

In the three following figures, the number in red (close to node_dn) is the number of this type of searche:

SRCH base="<suffix>" scope=2 filter="(|(attr_1=<node_dn>)..(attr_N=<node_dn))" attrs=ALL

Type 1

Membership graph

Type 2

Membership graph

Type 3

Membership graph

In conclusion:

A scalability issue exists because of the number of times the plugin searches the parents of the groups.

Let group_n be the ancestor (parent or grand parent…) of N descendants, it will trigger at least N searches (filter=”(|(attr_1=group_n)(attr_N=group_n))”). If during look up of a group, we can do a single search and cache the result, the next N-1 look up of that group will be satisfy without additional cost. It will reduce the cost of * look up * by 80% up to 85%

Graph loop: disable the cache

A corner case occurs when the update impacts a graph having a loop.

When there is a loop, the recursive fixup should stop but it also means the cached ancestors are invalid. For example let a MOD operation that ADD G2 and G3 as member of G1. While G1 was member of G2 and G3. With the status:

The fixup will start with G2. Ancestors of G2 are G4 plus ancestors of G1. It will search for ancestors of G1, that are ancestors of G2 and G3. It detects loop on G2 and skip ancestors of G2. Finally finds ancestors of G1 are {G2, G3, G5} and ancestors of G2 are {G4, G1, G3, G5}.

Now fixup of G3 finds ancestors of G1 in the cache and the result will be {G1, G2, G5}.

So G1 and G3, although they are in symmetrical situation have not the same number of ancestors because the ancestors of the first branch (G4->G2->G1) were skipped.

For loop detection and cache invalidation two new fields are added to the structure used in fixup see fixup get_groups.

keeping groups in the entry cache (ticket to be opened)

During internal searches, the candidates entries are retrieved from the entry cache and possibly reloaded from Database in case of cache miss. The lookup of parent groups requires to find/reload many groups into the entry cache. A typical group is a large entry with quite few attributes having a large set of values. Loading those entries is expensive (read of several overflow pages, allocation/sort of many member values).

When an entry gets to the lru it can get out of the entry cache. It would be benefical to delay a bit a group to get out of the entry cache. For example, we can imagine a counter on each entry in the lru. If the next entry to free, from the lru, is a group then increment the counter and move the entry to the begining of the lru. When the counter reaches a limit (e.g. 3) then the group is freed. When an entry goes entry_cache->lru, the counter is reset.

Implementation

48861 Prevent to fixup the same entry several times

The proposal for the ticket 48861 is to create a cache that will keep, for a given upddate the list of entries already fixup.

cache life cycle

The cache is hash table using the normalized group DN as a key.

The hash table is created at plugin startup and deleted at plugin stop.

The cache is emptied at the entrance of the plugin callback and also at the exit. So that each operation starts with a cleared cache. access (read/write) to the cache are protected with a Monitor lock memberof_operation_lock.

plugin callbacks are post-betxn so the membership attributes are not updated during its execution and cached values remain valid.

limitation

For remote backends, the cache is valid at the condition the remote entries are updated only by one instance.

performance

memory footprint

The cache will contains DNs. The DN in the cache are those of entry having already been fixup (memberof_fix_memberof_callback).

For example, assuming that each DN is 100 bytes long and there are 100 leafs for each group (in the last level), it will consum ~609*100=60K.

When running tests with create_test_data.py the memory footprint of instance with the cache was identical with instance without the cache.

throughput

see 49031 throughput

cache performance

see 49031 throughput

cache structure

The key and the value of each cached entry is its DN char pointer.

cache priming

The cache starts empty (see cache life cycle) at the memberof callback. Once lookdown has built the list of impacted nodes (leaf or groups), for each of them it will trigger a look up calling memberof_fix_memberof_callback.

Before fixing up the entry, memberof_fix_memberof_callback check if it has already been fixup (already in the hashtable). If this is the case it bailout, else it fixup the entry and add the DN in the cache.

scoping

no impact

49031 caching of groups ancestors

The proposal for the ticket 49031 is to create a cache that will keep, for a given group, the ancestors DNs of that group. Ancestors of non-group entries (leafs) are not keeped in that cache.

cache life cycle

The cache is hash table using the normalized group DN as a key.

The hash table is created at plugin startup and deleted at plugin stop.

The cache is emptied at the entrance of the plugin callback and also at the exit. So that each operation starts with a cleared cache. access (read/write) to the cache are protected with a Monitor lock memberof_operation_lock.

plugin callbacks are post-betxn so the membership attributes are not updated during its execution and cached values remain valid.

limitation

For remote backends, the cache is valid at the condition the remote entries are updated only by one instance.

performance

memory footprint

The cache will contains DNs. Those DNs are ancestors of a node that is a group.

An entry is a group if slapi_filter_test_simple(entry, config->group_filter)

We can expect that membership graph will look somehow like a tree, especially with much more leafs than intermediate nodes and more nodes at Depth D than at Depth D-1. The cache will be loaded only with intermediate nodes (i.e. groups) DNs.

For example, assuming that each DN is 100 bytes long,

When running tests with create_test_data.py the memory footprint of instance with the cache was identical with instance without the cache.

throughput

We are using create_test_data.py tool to measure the impact of the cache. This tool creates users/host/user group/hostgroup/sudo rules/hbac rules. It can be tuned to increase the number of leafs (hosts/users), the size of the groups and the nesting.

By default it creates :

The more there are leafs the more expensive it is. But number of leafs is NOT the major contributor. The tests were limited with very few leafs (5000 and 2000).

  duration with 5000 leafs duration with 1K leafs        
  and 1 member at level 4 and 20 members at level 4        
1.3.5 each group each rules total each group each rules total
vanilla 15 - 25s 48 - ? min 35h 27 - 74s 57-100min ~6days
+ 49031 6 - 16s 28 - ? min 20h - - -
+ 49031 + 48861 - - - 21-50s 2-4min 7h30

Conclusions: Adding a nested group with few members(20)

The test 49031 + 48861 was done with this configuration of create_test_data.py

users=1000,
groups=100,
groups_per_user=100,
nested_groups_max_level=2,
nested_groups_per_user=5,
hosts=1000,
hostgroups=100,
hostgroups_per_host=100,
nested_hostgroups_max_level=2,
nested_hostgroups_per_host=5,
direct_sudorules=5,  # users, hosts
indirect_sudorules=50,  # groups, hostgroups
sudorules_per_user=5,
sudorules_per_group=10,
sudorules_per_host=5,
sudorules_per_hostgroup=10,
direct_hbac=5,  # users, hosts
indirect_hbac=50,  # groups, hostgroups
hbac_per_user=5,
hbac_per_group=10,
hbac_per_host=5,
hbac_per_hostgroup=10

cache performance

The performance of the ancestor cache during group addition is in the table below. It is presented based on the nesting level.

Nesting level Hit ratio Op. duration cumul cache lookup
0 ~66% 6 - 16s 60ms
1-3 with low members 70-80% 6 - 16s 60ms
4 with 20 members >99% 2-4 min ~300ms

This shows that the cost of the cache has a not significant impact compare to the operation duration.

This shows that the more the groups are nested and populated with members the more the cache is saving internal searches.

cache structure

The data structure is

typedef struct _memberof_cached_value
{
    char *key;  /* when valid==0; pointer to the node DN used as hash key */
    char *group_dn_val;
    char *group_ndn_val;
    int valid;  /* when valid==1; group_dn/ndn are one ancestors of the node */
} memberof_cached_value;

The ancestors, of a given node, are stored in an array of ancestor DN/NDN.

When computing the ancestors of a given node, we need to merge ancestors of all its direct parents in a given set. An ancestor is present once in that set, so it requires to compare DN. This is the reason why NDN are also stored in the cache to avoid normalizing DN again and again.

A flag valid in the array indicates if we reach the end (valid==0) of the ancestors list. Slots with valid==1 contains effective ancestor in the DN/NDN.

A node can have no ancestor. To cache this the array element has NULL DN/NDN.

The ancestors of a node are stored using the node DN as the key. When freeing the ancestors of that node, the key is stored at the end of the list. So the array element with valid==0 contains key that is pointer to the node DN.

fixup get_groups structure

The data structure used during recursive call to identify ancestors is enhanced

 typedef struct _memberof_get_groups_data
 {
         MemberOfConfig *config;
         Slapi_Value *memberdn_val;
         Slapi_ValueSet **groupvals;
         Slapi_ValueSet **group_norm_vals;
         Slapi_ValueSet **already_seen_ndn_vals; /* NEW to detect loops */
         PRBool use_cache; /* NEW to invalidate the cache */
 } memberof_get_groups_data;

Two new fields are reguired. already_seen_ndn_vals is the set of nodes found during the look up. groupvals and group_norm_vals are new valuesets at each level of the graph, while already_seen_ndn_vals and use_cache are the same fields passed throught all recursive calls.

cache priming

The cache starts empty (see cache life cycle) at the memberof callback. Once lookdown has built the list of impacted nodes (leaf or groups), for each of them it will trigger a look up calling memberof_fix_memberof_callback.

The function that actually implements the look up is memberof_get_groups_r that computes the set of ancestors of a given node. If the set is already caches it is used else it is computed (memberof_call_foreach_dn) and then cached.

At this point leaf ancestors as well as grooup ancestors are cached as it is not possible to know if the node is a group or not. In memberof_fix_memberof_callback, after memberof_get_groups_r has returned (and cache the ancestor of the node), if the node is not a group then its cached ancestors are removed from the cache.

scoping

If the node is in excluded scopes or not in scopes (if scopes are defined), memberof_call_foreach_dn should not lookup the cache or do an internal search to retrieve its parent.

Major Configuration options

Replication

The proposed changes have no impact in the way replication is managing memberof updates. Each update of memberof attribute, will go into the changelog. Replication agreement will replicate those updates unless they are skipped.

updates and Upgrades

None

Dependencies

None

Last modified on 2 April 2024